关于数据类型精度问题几个问题

艺帆风顺 发布于 2025-04-03 24 次阅读

⭐C# 常用数字类型在C#中，常用的数字类型包括整数类型和浮点数类型。每种类型都有其特定的用途和适用场景。下面列出了C#中最常用的数字类型及其特点：

🌟整数类型

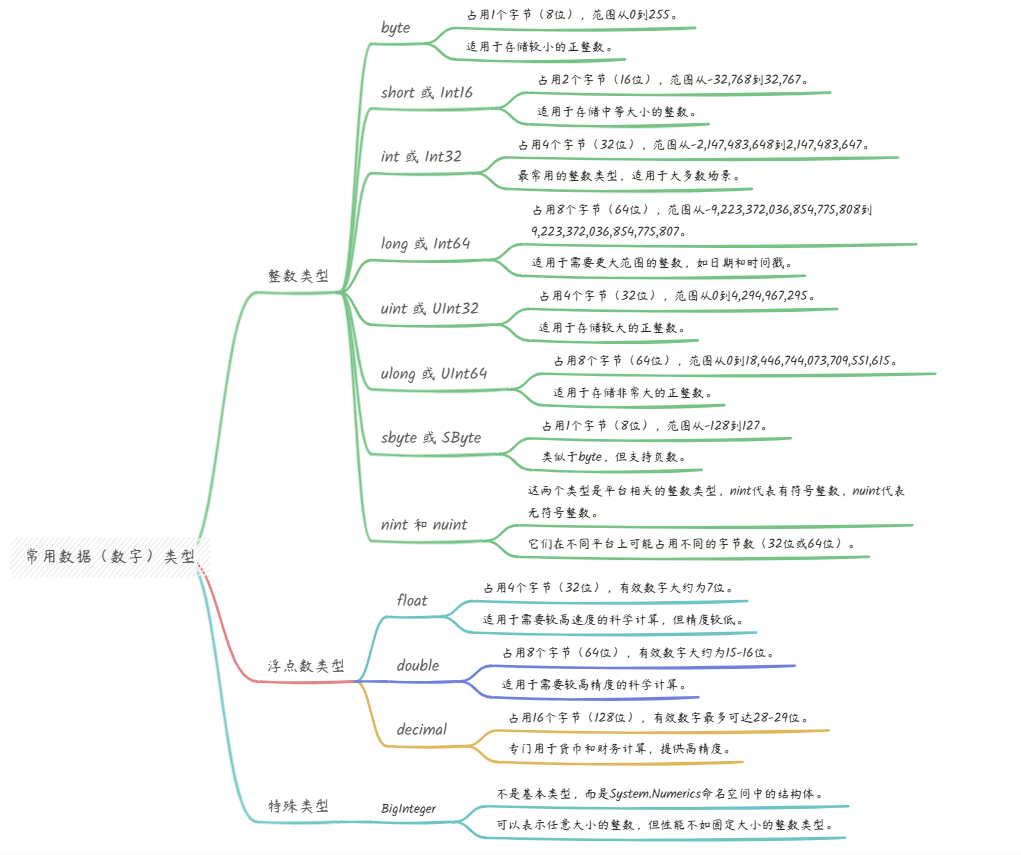
●byte:○占用1个字节（8位），范围从0到255。○适用于存储较小的正整数。●short或Int16:○占用2个字节（16位），范围从-32,768到32,767。○适用于存储中等大小的整数。●int或Int32:○占用4个字节（32位），范围从-2,147,483,648到2,147,483,647。○最常用的整数类型，适用于大多数场景。●long或Int64:○占用8个字节（64位），范围从-9,223,372,036,854,775,808到9,223,372,036,854,775,807。○适用于需要更大范围的整数，如日期和时间戳。●uint或UInt32:○占用4个字节（32位），范围从0到4,294,967,295。○适用于存储较大的正整数。●ulong或UInt64:○占用8个字节（64位），范围从0到18,446,744,073,709,551,615。○适用于存储非常大的正整数。●sbyte或SByte:○占用1个字节（8位），范围从-128到127。○类似于byte，但支持负数。●nint和nuint:○这两个类型是平台相关的整数类型，nint代表有符号整数，nuint代表无符号整数。○它们在不同平台上可能占用不同的字节数（32位或64位）。🌟浮点数类型●float:○占用4个字节（32位），有效数字大约为7位。○适用于需要较高速度的科学计算，但精度较低。●double:○占用8个字节（64位），有效数字大约为15-16位。○适用于需要较高精度的科学计算。●decimal:○占用16个字节（128位），有效数字最多可达28-29位。○专门用于货币和财务计算，提供高精度。🌟特殊类型●BigInteger:○不是基本类型，而是System.Numerics命名空间中的结构体。○可以表示任意大小的整数，但性能不如固定大小的整数类型。🌟示例代码下面是一个简单的示例，演示如何使用这些数字类型：

    using System;class Program{    static void Main()    {        byte byteValue = 100;        short shortValue = 5000;        int intValue = 1_000_000;        long longValue = 100_000_000_000L;        float floatValue = 3.141592f;        double doubleValue = 2.718281828459045;        decimal decimalValue = 1.99m;        Console.WriteLine($"Byte Value: {byteValue}");        Console.WriteLine($"Short Value: {shortValue}");        Console.WriteLine($"Int Value: {intValue}");        Console.WriteLine($"Long Value: {longValue}");        Console.WriteLine($"Float Value: {floatValue}");        Console.WriteLine($"Double Value: {doubleValue}");        Console.WriteLine($"Decimal Value: {decimalValue}");    }}
    这个示例展示了如何声明和初始化不同类型的数值，并打印它们的值。总结来说，根据你的需求选择合适的数字类型是非常重要的。对于财务和货币计算，decimal类型通常是最佳选择；对于科学计算，double通常足够用；而对于一般用途的整数操作，int是最常用的选择。⭐C# 处理货币，财务，等数据，什么数据类型合适在C#中处理货币、财务和其他需要高精度的数据时，最适合使用的数据类型是decimal。decimal类型专为金融和货币计算设计，它提供了高达28-29位的有效数字，并且专门针对十进制数进行了优化，以确保精度。以下是选择decimal类型的一些理由：1精度：decimal类型可以提供28-29位的有效数字，这对于财务和货币计算来说通常是足够的。相比之下，float和double类型分别只能提供7位和15-16位的有效数字，并且它们在处理十进制数时可能会产生精度问题。2十进制数的精确表示：decimal类型能够精确表示十进制数，这对于货币计算非常重要。例如，0.1可以在decimal类型中得到精确表示，而在float或double类型中，0.1是一个无限循环小数，只能近似表示。3避免累积误差： 在涉及多次计算的情况下，使用decimal类型可以减少累积误差的可能性，这对于需要高度精确的财务计算尤为重要。4运算符重载：decimal类型支持各种数学运算符，并且.NET Framework提供了许多针对decimal类型的方法，使得货币和财务计算变得更加简单和直观。5文化敏感性：decimal类型支持文化敏感的操作，例如在不同的地区有不同的货币格式，decimal类型可以更好地处理这些情况。下面是使用decimal类型处理货币和财务数据的示例：
      using System;class Program{    static void Main()    {        decimal price = 19.99m; // 使用'm'后缀指定decimal类型的数值        decimal quantity = 5m;        decimal total = price * quantity;        Console.WriteLine($"Price: {price:C}");        Console.WriteLine($"Quantity: {quantity:N0}");        Console.WriteLine($"Total: {total:C}");    }}
      在这个示例中，我们定义了商品的价格和数量，然后计算了总价。decimal类型的变量price和quantity用于存储货币值。我们还使用了格式化字符串{price:C}来格式化输出为货币格式。总之，对于需要高精度的财务和货币计算，decimal类型是最佳选择。它不仅可以确保数据的准确性，还可以简化财务计算的过程。🌟C# 金额处理为什么不使用 int在C#中处理金额时通常不使用int类型的原因是，金额通常需要更精确的表示，包括小数部分。int是一个整数类型，它不能存储小数点后的数值，因此对于需要精确到分甚至更小单位的金融计算来说，int是不够用的。对于金额处理，C#中推荐使用decimal类型。decimal类型可以提供高达28-29位的有效数字，并且专门设计用于金融和货币计算，能够避免浮点数（如float或double）常见的精度问题。例如，在进行加减乘除运算时，decimal类型能确保结果的准确性，这对于财务应用至关重要，因为即使是极小的误差也可能导致巨大的财务差异。此外，decimal类型还支持一些货币相关的运算符和方法，使其更加适合于货币值的处理。使用int来表示金额的一个常见做法是在某些特定场景下，比如将金额以分为单位存储（例如，1.50美元存储为150）。但这仍然需要在逻辑层面上转换为decimal或其他浮点类型进行显示或计算，以保持精度。这种方法在不需要进行复杂计算的情况下有时会被采用，以减少存储空间的需求。但是，为了保证数据的准确性和一致性，对于涉及金额的计算和存储，还是推荐使用decimal。🌟int 精度问题举例int类型在C#中是一个32位的整数类型，它可以存储从-2,147,483,648到2,147,483,647之间的任何整数值。int类型本身并不涉及精度问题，因为它只处理整数，没有小数部分。不过，使用int时可能会遇到以下几种情况，这些情况可能被误解为精度问题：1溢出：如果你试图存储一个超出int范围的值，将会发生溢出。这意味着如果一个值太大或太小而无法被int表示，编译器会将其“循环”回可表示的范围内，导致错误的结果。例如，如果你尝试将int.MaxValue + 1赋值给一个int类型的变量，其结果将是int.MinValue。2小数点舍入：当你需要处理包含小数的数值时，使用int会导致信息丢失。例如，将3.14赋值给一个int类型的变量将只保留3，小数点后的部分会被丢弃。这并不是精度问题，而是int类型的设计目的不是为了处理非整数值。3与其他类型的交互：当int类型与float或double类型进行数学运算时，可能会引入浮点数的精度问题。这是因为float和double类型虽然可以表示小数，但它们使用二进制浮点数表示法，对于某些十进制小数（如0.1）并不能精确表示，从而可能导致计算结果的误差。下面是一些具体的例子来说明上述情况：1溢出示例
        int maxInt = int.MaxValue;int overflowExample = maxInt + 1;Console.WriteLine("Overflow Example: " + overflowExample); // 输出: -2147483648
        在这个例子中，maxInt的值是int.MaxValue，即2,147,483,647。当我们尝试将其增加1时，由于int类型的最大值已经被达到，因此结果将会溢出，变为int.MinValue，即-2,147,483,648。2小数点舍入示例
          double numberWithDecimal = 3.14;int integerPart = (int)numberWithDecimal;Console.WriteLine("Integer Part: " + integerPart); // 输出: 3
          在这个例子中，我们将带有小数部分的double类型的值转换为int类型。int类型只会保留整数部分，小数点后的部分将被丢弃。3与其他类型的交互示例
            int intNumber = 3;double doubleNumber = 0.1;double result = intNumber * doubleNumber;Console.WriteLine("Result: " + result); // 输出: 0.3
            在这个例子中，虽然结果看起来正确，但实际上由于doubleNumber（0.1）在二进制中的表示是一个近似值，因此最终的result可能不是一个精确的0.3。虽然这种情况不直接涉及int类型的精度问题，但它展示了在与其他类型（如double）进行运算时可能出现的精度问题。总结来说，int类型本身不会出现精度问题，但在使用过程中需要注意其范围限制以及与其他类型进行运算时可能引入的精度问题。🌟double精度问题举例double类型在C#中是一个双精度64位浮点数，它能够表示非常大或非常小的数值，有效数字大约有15到16位。尽管double提供了比float更大的范围和更高的精度，但在处理某些数值时，它仍然存在精度问题，尤其是在涉及到小数点后多位数的计算时。double的精度问题主要来源于它的内部表示方式。double使用IEEE 754标准的二进制浮点数格式，这种格式在处理大多数十进制小数时，无法精确表示，因为很多常见的十进制分数（如0.1、0.2等）在二进制中是无限循环小数。这意味着即使是很简单的十进制数，当转换成double类型时，也可能会变成一个近似值，而不是精确值。例如，当你执行如下代码：
              double a = 0.1;double b = 0.2;double sum = a + b;Console.WriteLine(sum);
              理论上sum应该是0.3，但由于精度问题，实际输出可能是类似0.30000000000000004这样的值。在处理货币、财务数据或需要高精度计算的场景中，这种精度问题可能会造成重大影响。为了避免这类问题，C#中的decimal类型被设计出来，它使用128位来存储数值，可以提供最多28-29位的有效数字，并且专门针对十进制数进行了优化，非常适合处理货币和财务数据。因此，当处理需要精确到小数点后几位的数值时，应该优先考虑使用decimal类型，而不是double或float。在其他情况下，如科学计算或对精度要求不高的场景，double则是一个合理的选择。🌟float 精度问题 举例float类型在C#中是一个单精度32位浮点数，它使用IEEE 754标准的浮点数表示法。float类型可以表示很大或很小的数值，但是由于其内部表示的限制，它在处理某些十进制小数时会出现精度问题。这是因为很多十进制小数在二进制中无法被精确表示，只能近似。例如，十进制数0.1在二进制中是一个无限循环小数，这就意味着当它被转换为float类型时，它会被截断或四舍五入，导致一个近似值而非精确值。下面是一个具体的示例：
                float a = 0.1f; // 注意这里的'f'后缀，它告诉编译器这是一个float类型的字面量float b = 0.2f;float sum = a + b;Console.WriteLine("Sum: " + sum); // 输出可能不是预期的0.3Console.WriteLine("Sum as decimal: " + (decimal)sum); // 使用(decimal)强制转换查看更详细的数值
                当你运行这段代码时，你可能会看到输出结果并非精确的0.3。实际上，sum的值可能是0.30000005或者类似的值，具体取决于计算机和编译器的具体实现细节。这种精度问题在涉及小数点后多位的计算中尤其明显，例如：
                  float result = 0.1f + 0.1f + 0.1f - 0.3f;Console.WriteLine("Result: " + result); // 可能输出一个非零的小数，如2.77555756156289E-08
                  在这个例子中，即使数学上计算结果应该是0，但由于float类型的精度限制，最终结果可能是一个非常接近零但不等于零的数。为了避免这类精度问题，对于需要高精度的计算，如财务计算，应使用decimal类型。如果在不需要很高精度的科学计算中使用float，则需要了解并接受这种精度上的局限性。🌟decimal 精度问题举例decimal类型在C#中是一个128位的数据类型，专门用于处理需要高精度的数值，如货币和财务数据。它提供了最多28-29位的有效数字，并且在处理十进制数时比float和double更为准确。尽管decimal类型非常适合处理需要高精度的数值，但在某些极端情况下，它仍然可能存在精度问题。这里有几个可能的情况：1超出表示范围：decimal类型的表示范围是有限的，尽管非常大。如果一个数值超出了decimal类型所能表示的最大或最小值，那么就会发生溢出。2运算中的累积误差：虽然decimal类型的精度非常高，但在大量复杂的运算中，小数点后的累积误差仍有可能逐渐积累起来。虽然这种情况非常罕见，但对于涉及大量迭代运算的应用程序而言，仍需注意。3表示非十进制小数：尽管decimal类型非常适合表示十进制数，但对于某些非十进制小数，它可能仍然无法提供完全精确的表示。例如，某些分数在十进制表示中是无限循环的，即便使用decimal也可能无法完全精确地表示。下面是一些具体的示例来说明这些情况：1超出表示范围示例
                    decimal maxDecimal = decimal.MaxValue;decimal overflowExample = maxDecimal + 1m;Console.WriteLine("Overflow Example: " + overflowExample); // 输出: -79228162514264337593543950335

                    在这个例子中，maxDecimal的值是decimal.MaxValue，即79,228,162,514,264,337,593,543,950,335。当我们尝试将其增加1时，由于decimal类型的最大值已经被达到，因此结果将会溢出，变为负数。2运算中的累积误差示例虽然这种情况比较少见，但如果进行大量的连续运算，可能会出现累积误差。例如：

                      decimal oneThird = 1m / 3m;decimal result = oneThird * 3m;Console.WriteLine("Result: " + result); // 输出: 1

                      在这个例子中，尽管decimal类型可以很好地处理1/3的运算，但在实际中，1/3是一个无限循环小数。尽管最终结果是1，但在某些复杂的连续运算中，这种非精确表示可能会导致最终结果出现细微的误差。3表示非十进制小数示例

                        decimal pi = 3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679m;decimal piSquared = pi * pi;Console.WriteLine("Pi Squared: " + piSquared);

                        在这个例子中，我们尝试计算π的平方。虽然decimal类型可以提供非常高的精度，但对于π这样无限不循环的常数，仍然无法提供完全精确的表示。因此，计算π的平方可能会引入轻微的误差。总结来说，decimal类型非常适合处理货币和财务数据，但在某些极端情况下，仍然可能出现精度问题。然而，这些情况在实际应用中非常罕见，对于绝大多数财务计算来说，decimal类型提供的精度已经足够。

                        若有收获，就点个赞吧